Personal Perspective

Basic Optimization

최적화에 대한 기초적인 내용을 다뤄보자.

Exploring Model Space

모델 공간에 대해 곱씹어보자.

동전을 천 번 던졌을 때 생기는 모델 공간에 대해 고민해보자. 동전이 앞면이 나올 확률이 모델을 결정하고 거기에 대응되는 likelihood가 합쳐져 모델과 likelihood가 이루는 지형landscape이 만들어진다. 이는 2차원 평면 위에 그려볼 수 있다.

np.random.seed(42)
p = 0.73
flips = np.random.binomial(1, p, size=1000)

def loglikelihood(data, theta):
    if theta == 0 or theta == 1:
        return -np.Infinity
    return (np.sum(data) * np.log(theta) + (len(data) - np.sum(data)) * np.log(1 - theta))

print(np.sum(flips))  # 739

# fitness landscape
axis = np.arange(0, 1, 0.01)
plt.plot(axis, [loglikelihood(flips, x) for x in axis], label="Loglikelihood")
plt.axvline(p, color='r', label='Ground Truth')
plt.legend()
plt.show()

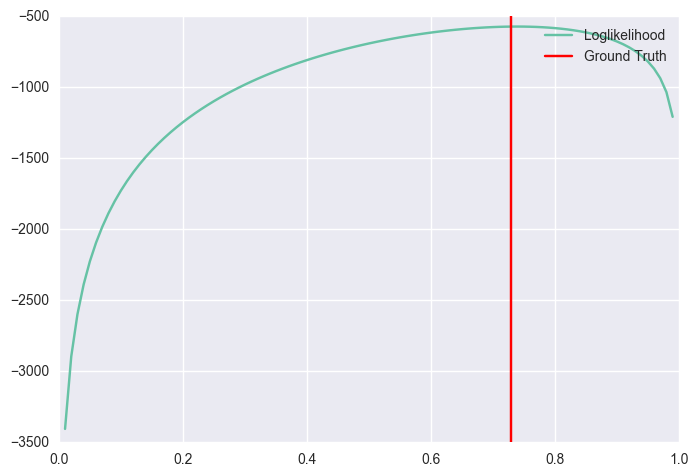
Point estimation, 특히 MLE는 위의 log likelihood를 최대화하는 모델을 찾게 된다. 즉, 이런 식으로 학습 문제를 최적화 문제로 변환하여 접근하는 것이 가능하다.

$$\hat{p} = \mathrm{argmax}_p p^k (1 - p)^{n - k} = \mathrm{argmax}_p k \log p + (n - k) \log (1 - p)$$

이렇게 찾은 $\hat{p}$는 모델 공간의 한 점이다. 이 문제에 접근하는 방법은 여러 가지 있다.

미분

함수의 최대/최소는 미분을 통해 찾을 수 있다.

\begin{align} \frac{d(p^k (1-p)^{n-k})}{dp} &= k p^{k-1} (1-p)^{n-k} - (n-k)(1-p)^{n-k-1} p^k \\ &= p^{k-1} (1-p)^{n-k-1} (k (1-p) - (n-k)p)\\ \end{align}

미분값이 0이 되는 지점이 최대/최소일 것이므로 아래와 같은 결과를 얻는다.

\begin{align} (k (1-p) - (n-k)p) &= 0 \\ k - kp - np + kp &= 0 \\ p &= \frac{k}{n} \end{align}

즉, likelihood를 극대화하는 점은 $\frac{k}{n}$인 지점이다. 이는 직관이 알려주는 전체 동전을 던진 횟수 분에 앞면이 나온 횟수를 사용하는 것과 일치한다. 다만 엄밀하게는 이게 실제로 최대값인지 확인하기 위해 2계 도함수를 따져봐야 한다.

Gradient Descent

보통 접하게 되는 문제는 위와 같은 방식으로 미분을 통해 한 번에 풀 수가 없다. 대신 임의의 점을 잡고 거기에서 미분값을 구해서 조금씩 이동하는 방식으로 접근하게 된다. 미분해서 구한 방향이 함수가 증가하는 방향이고 그 크기가 얼마나 빠르게 증가하는지 알려주므로 최대화는 해당 방향으로, 최소화는 반대 방향으로 조금 이동하면 된다. 이 접근 방법은 다루는 함수가 적당히 미분가능하다는 가정을 해야 하지만 많은 경우 이를 만족한다.

# gradient descent
# divide by data size for convenience
def grad(data, theta):
    return -(np.sum(data) / theta - (len(data) - np.sum(data)) / (1 - theta)) / len(data)

theta_hat = 0.1
stepsize = 0.001

theta_list = [theta_hat]
for k in range(1500):
    theta_delta = grad(flips, theta_hat)
    theta_hat -= stepsize * theta_delta
    theta_list.append(theta_hat)

print(theta_hat)  # 0.738556865373

잘 살펴보면 위의 gradient 계산은 전체 데이터에 대해 한 것이다. 다만 그 크기가 폭발하지 않도록 데이터 크기로 나눠주는 보정을 하였다. 우리가 애초에 최대화하고 싶은 것은 관측한 전체 데이터에 대한 likelihood 이므로 gradient도 전체 데이터를 사용하는 것이 맞다.

임의의 점에서 출발하여 관측한 데이터의 likelihood를 최대화하는 방향으로 점점 모델이 이동하는 것을 볼 수 있다.

Stochastic Gradient Descent

Gradient descent의 문제는 전체 데이터를 살펴봐야 하는 것이다. 만약 데이터가 아주 많다면 매 번 gradient 반대 방향으로 이동하기 위해 데이터를 전부 살펴봐야 하는데 이는 비현실적이다. 다행히도 데이터를 일부만 사용해서 gradient를 계산하고 이를 따라가더라도 원하는 결과를 얻을 수 있음이 알려져 있다. 다만 데이터에 특별한 편향이 없도록 주의해야 한다.

def sgd_grad(x, theta):
    return -(x / theta - (1 - x) / (1 - theta))

theta_hat = 0.1
stepsize = 0.001

theta_list = [theta_hat]
for k in range(10):
    for d in flips:
        theta_delta = sgd_grad(d, theta_hat)
        theta_hat -= stepsize * theta_delta
        theta_list.append(theta_hat)

print(theta_hat)

위의 gradient descent와는 다르게 모델의 변화가 매끄럽지 않은 것이 보인다. 하지만 결국 원하는 지점으로 도달하는 것도 확인할 수 있다.

위의 예제에서는 문제가 convex하지만 모든 문제가 그렇지는 않다. Non-convex한 문제를 다룰 때에는 이렇게 찾은 해는 지역 최적점local optimum일 뿐, 전역 최적점global optimum이라는 보장이 없다. 또한 항상 gradient 정보를 얻을 수 있는 것도 아니다. 가령 모델 공간이 이산적discrete이라면 gradient를 얻을 수 없다. 이런 경우에는 다른 접근을 취해야만 한다. 대체로 이런 non-convex하거나 조합적combinatorial인 문제는 풀기 쉽지 않다.

Second Order Approximation of Objective Landscape

Gradient descent에 대해 조금 더 알아보기 위해 기존 함수를 Taylor 전개를 통해 2차 함수로 근사하는 것을 살펴보자.

$$f(z) \approx f(z_0) + \nabla f(z_0)^T (z - z_0) + \frac{1}{2}(z - z_0)^T H (z - z_0)$$

여기에서 $\nabla f(z_0)$는 gradient 벡터, $H$는 $z_0$에서의 Hessian 행렬이다.

위의 결과로 나오는 2차 함수의 2차식 부분을 살펴보자. 모델의 공간이 $x, y$의 두 차원으로 이루어져 있다고 가정해보자.

만약 $H$가 단위행렬에 비례하면,

$$\left[ \begin{array}{cc} x & y \\ \end{array} \right] \begin{bmatrix} a & 0 \\ 0 & a \\ \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = a(x^2 + y^2) $$

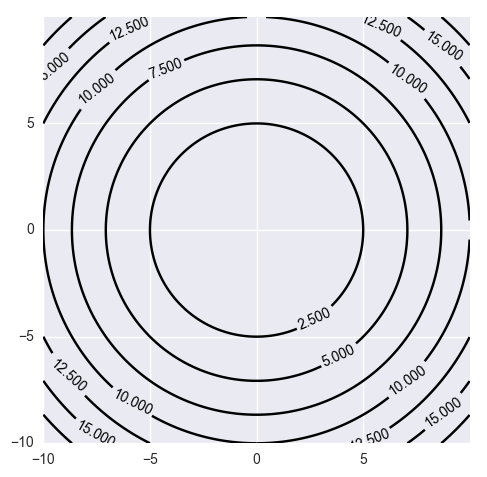
$H$가 대각행렬diagonal matrix이면,

$$\left[ \begin{array}{cc} x & y \\ \end{array} \right] \begin{bmatrix} a & 0 \\ 0 & b \\ \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = ax^2 + by^2 $$

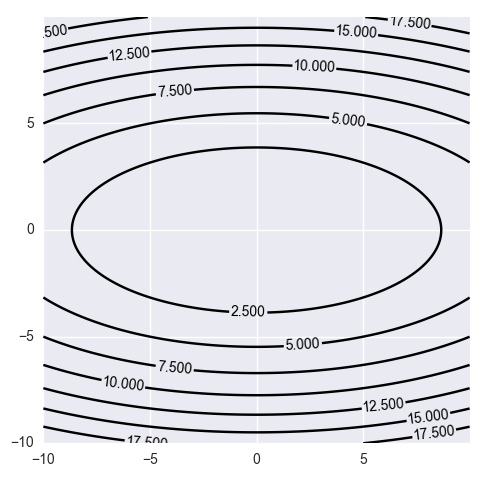
$H$가 일반적인 행렬이라면 아래와 같은 모습의 지형을 띈다.

$$\left[ \begin{array}{cc} x & y \\ \end{array} \right] \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} = ax^2 + dy^2 + (b + c)xy $$

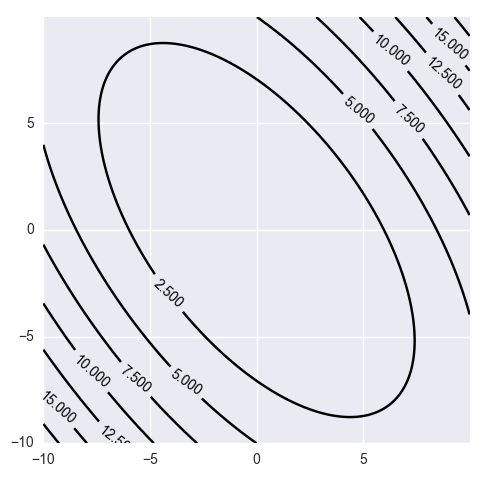
Hessian이 곡률 정보를 담고 있다는 표현을 사용하는데, 위의 등고선을 살펴보면 그 느낌을 알 수 있다. 원래의 문제 공간은 복잡한 모양의 등고선으로 표현될 수도 있을 텐데, 위의 근사는 현재 주어진 점에서 이런 곡률 정보를 잘 근사하는 등고선으로 주변을 표현하는 것이라 생각할 수 있다.

Newton's Method

이제 근사 함수를 사용해 최적화 문제를 풀어보자. 위의 예제에서 gradient와 Hessian을 구해보면 아래와 같다.

def grad(data, theta):
    return (np.sum(data) / theta - (len(data) - np.sum(data)) / (1 - theta))

def hessian(data, theta):
    return (-np.sum(data) / (theta**2) - (len(data) - np.sum(data)) / ((1 - theta) ** 2))

def approx(z, x):
    return loglikelihood(flips, x) + grad(flips, x) * (z - x) + 1/2 * hessian(flips, x) * (z - x)**2

axis = np.arange(0, 1, 0.01)
plt.plot(axis, [loglikelihood(flips, x) for x in axis], label="Loglikelihood")

newaxis = np.arange(0.01, 0.99, 0.01)
p_hat = 0.1
plt.plot(newaxis, np.array([approx(x, p_hat) for x in newaxis]),
         'g-', linewidth=1, label='Approximated Function')
plt.plot([p_hat, p_hat], [-3.5, -0.5], label='Current Point')
plt.plot([p_hat - grad(flips, p_hat)/hessian(flips, p_hat),
         p_hat - grad(flips, p_hat)/hessian(flips, p_hat)],
         [-3.5, -0.5], label='Proposed Point')
plt.ylim(-3.5, -0.5)
plt.legend(loc=4)

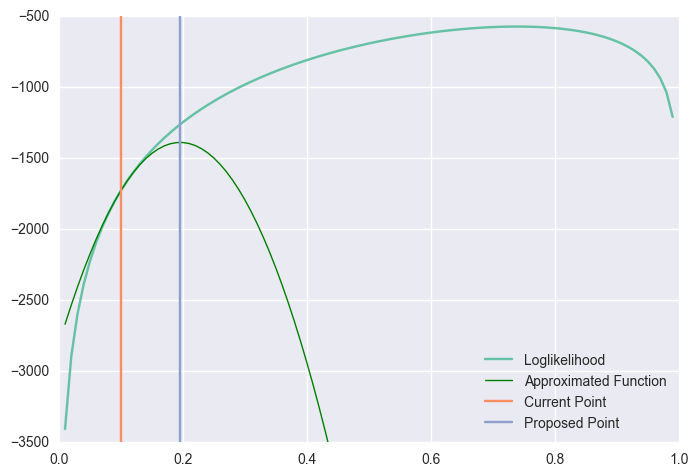
이렇게 근사한 함수에서 극점의 위치는 gradient가 0인 지점이다.

$$\nabla f(z_0) + H (z - z_0) = 0$$

$z$에 대해 풀어보면,

$$z = z_0 - H^{-1} \nabla f(z_0)$$

를 얻을 수 있다. 위의 그림에서 proposed point의 위치는 정확히 이 방법을 사용해서 구한 것이다. 위의 업데이트 규칙을 반복적으로 적용하면 아래와 같은 방식으로 최적화가 진행된다.

위의 과정을 풀어서 설명하면, 현재의 위치에서 원래의 목적함수를 가장 비슷한 2차 함수로 근사한 뒤, 해당 2차 함수의 극점으로 옮겨가는 것을 반복하는 것이다. 이런 방식으로 임의의 점에서 출발하여 gradient와 Hessian 정보를 사용하여 다음 점으로 업데이트 하는 것을 Newton's method라 한다. 이 방법은 quadratic convergence rate를 갖는데, 매 반복마다 정확히 맞춘 significant digit이 두 배 정도 증가한다. 그러므로 사실상 이보다 더 빠른 수렴 속도를 달성할 필요는 크지 않다. 다만 이 접근은 극점을 찾는 것이므로 non-convex한 문제를 다룰 때에는 반대 방향으로 가지 않도록 주의해야 한다.

Newton's method는 좋은 결과를 내지만 Hessian의 역행렬을 구하는 것은 매우 비싸다. 그 뿐만이 아니라 $n$ 개의 변수를 다룬다면 Hessian은 $n^2$ 개에 비례하는 저장공간이 필요하다. 수백만 차원의 모델 공간도 다루는 현대에는 비현실적인 요구사항이다. 그래서 Hessian을 근사하는 다양한 기법이 있다.

First Order Method

위의 관점에서 gradient descent를 다시 살펴보자.

$$z = z_0 - \alpha \nabla f(z_0)$$

이 식을 Newton's method의 업데이트 식과 비교해보면 Hessian 행렬을 $\frac{1}{\alpha} I$로 근사한 것임을 알 수 있다. 즉, 현재 위치에서 지형의 곡률을 무시한 채 이동하는 것이 된다.

단순한 gradient descent는 위와 같이 곡률 정보를 무시하기 때문에 아래와 같은 지그재그 모양의 움직임을 보일 수 있다.

이를 해결하는 한 가지 방법으로 지금까지 이동하던 경향을 고려한 업데이트 규칙을 생각해볼 수 있다.

$$z_{k + 1} = z_k - \alpha \nabla f(z_k) + \beta (z_k - z_{k - 1})$$

이를 heavy ball method 혹은 momentum method라 부른다. 이렇게 되면 위와 같은 지그재그 모양의 움직임을 많이 완화하고 더욱 빠르게 지역 최적점으로 수렴할 수 있다.

Feature Preprocessing

위의 직관을 갖고 데이터에 필요한 전처리 과정을 생각해보자. 2 차원 피쳐가 주어졌을 때의 최적화 문제를 고려해보자. 가령 모델은 $h = w_1 x_1 + w_2 x_2$ 꼴로 주어지고, $(w_1 x_1 + w_2 x_2 - y)^2$를 최소화하는 것이 목표라고 하자.

$l = w_1 x_1 + w_2 x_2 - y$로 놓으면 이는 하나의 직선을 나타낸다. 가령 두 개의 데이터 $d^{(1)}: ( (1, 1), 1)$, $d^{(2)}: ( (1, -1), 0)$이 있다면 에러의 등고선은 아래와 같이 그려진다.

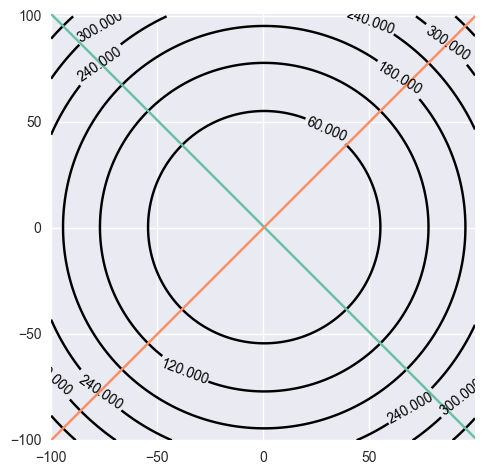
SGD를 사용하여 위의 에러 등고선 위를 탐색한다고 가정하자. 그렇다면 매번 하나의 직선과 그에 대응되는 등고선만 보이는 셈이므로 매 반복마다 아래와 같은 에러 등고선을 보게 된다.

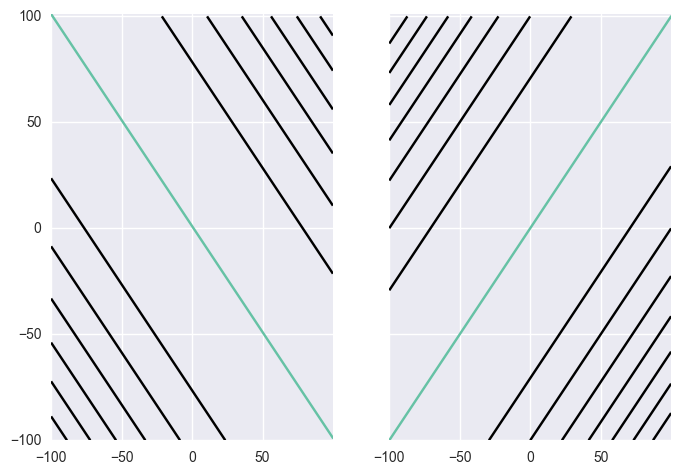
이 문제에서 gradient 방향으로 정확히 정해진만큼 뛸 수 있다고 가정하면 매번 해당 직선과 수직이 되도록 이동하여 도달할 것이다. 만약 이 때 데이터가 $d^{(1)}: ( (101, 101), 1)$, $d^{(2)}: ( (101, 99), 0)$로 주어진다면 두 직선이 거의 평행한 꼴이 된다. 그렇다면 위의 논리 전개에 의해 앞서 살펴보면 지그재그와 비슷하게 진동하는 모습을 보이게 될 것이다. 이를 완화하는 방법으로 데이터에서 각각 평균을 빼주는 것이 있다. 그렇다면 데이터는 $d^{(1')} = ((1, 1), 1)$, $d^{(2')} = ((1, -1), 0)$로 변하고 이렇게 되면 보다 안정적인 수렴이 가능하다.

두 피쳐의 크기가 확연하게 다를 때에도 비슷한 문제가 생긴다. $d^{(1)} = ((0.1, 10), 1 )$, $d^{(2)} = ((0.1, -10), 0)$로 주어진다면 아래와 같은 모습이 되는데, 이는 각 피쳐가 비슷한 구간에 갇히도록 표준편차로 나누는 작업을 하는 것이 흔하다.

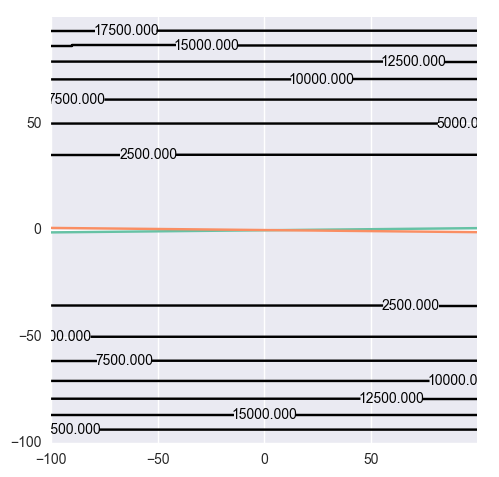
그러면 다시 데이터는 $d^{(1')} = ((1, 1), 1)$, $d^{(2')} = ((1, -1), 0)$와 같이 변한다.

위의 평균으로 빼고 표준편차로 나누는 과정을 정규화standardization라 한다. 정규화라는 표현은 다양하게 쓰여서 문맥에 맞춰 의미를 파악해야 한다.

비슷한 논리로 인해 gradient 반대 방향으로 얼마나 많이 뛰어야 하는지를 결정하는 learning rate/step size도 그 크기를 잘 결정해야 한다. 또한 모델의 초기 시작점의 선택도 중요하다.

References

Hessian 근사는 finite difference를 쓰는 방법이나, 지금까지의 gradient 정보를 바탕으로 근사하는 방법인 quasi-Newton method 등 다양하다. 최적화에 대해 더 자세히 알고 싶다면 Stephen Wright의 MLSS 2013 Optimization 강의를 살펴보기 바란다.

위의 피쳐 변환과 관련된 내용은 Hinton의 coursera 강의와 Léon Bottou의 MLSS 2013 Multilayer Networks 강의를 참고하였다.

최근 기계 학습의 활발한 연구로 다양한 최적화 기법이 등장하고 있다. 이에 대한 간략한 소개는 Sebastian Ruder의 An overview of gradient descent optimization algorithms를 살펴보기 바란다.